I used Machine Learning to Beat the Roblox Interview Game

The Challenge

Unlike most other companies, Roblox takes a bit of a different approach when it comes to interviews. Instead of the classic Leetcode coding style assessments, they use problem solving games. One of these games is called Kaiju Cats. It's a game where you control the movement of 3 cats and try to maximize the amount of points they get as they move around the board.

After learning about popular machine learning algorithms like Deep Blue and Alpha Go in my university class, I wanted to create something similar that could learn and master this game. I was initially thinking of using a reinforcement approach: simulate millions of games and use either random forest or a neural net style algorithm to develop heuristics for solving games.

Rules of the Game

The primary objective is to maximize the combined power of three cats within a hard limit of 15 turns. Player actions are defined by attaching commands to "Attachment Points" on building floors, which directs the cats' movement through the city. Cats gain fixed power values for destroying standard building floors, but can also destroy "Power Plants" to double their current power. The grid also features traps that modify a cat's state or score: Mud (stuck for one turn), Spike Traps (halves current power), and Boulders (reverses direction). The game concludes as cats reach their matching beds, applying a critical, order-based bonus: the first cat gets +2,000 power, the second multiplies its power by 3, and the third multiplies its power by 5.

You can play the game on Roblox here: https://www.roblox.com/games/13977123257/Kaiju-Cats

Is This Even Possible?

To start off, I had to ask myself the question of is this even possible? Upon my quick initial count there are 25-30 squares where you can place movement tiles (I later found out it's 31!). Also we are looking for the permutations here not combinations: (Left, Stomp, Right) is going to be very different from (Right, Stomp, Left) even though they use the same commands.

Since each tile can be one of 6 commands (up, down, left, right, stomp, powerup), that's 6 possible choices for each square. I assumed 30 just for simplicity.

Assuming 30 tiles for simplicity, that means there are 6³⁰ possible command arrangements.

Yeah not a good initial sign…

But, before I threw this project away as impossible, I considered chess algorithms. The average branching factor, or the number of possible moves for each chess move, is 35. That's a lot worse than 6. Basic chess algorithms written by amateurs are able to play at a beginner to intermediate level. So why couldn't I devise a Kaiju engine that could play at an equally beginner to intermediate level?

My First Approach

My first challenge in this project was how to even approach the problem. Could it even be solved? As with all machine learning, I started to think about what would be the goal metric? How could I measure how good my algorithm was performing? How would I prune off combinations of movements from the game, as searching all of them was infeasible?

The Problems

There were several problems with this approach:

The game map changes with each play. This means that some heuristics which work well on some maps might not work on other maps.

Machine learning algorithms require huge datasets. There is no automated way to run the game millions of times, so how could I gather a large enough dataset to make any ML algorithm work?

The most obvious of these problems was that since this was a game designed to be played by people, there was no way to run this game millions (if not more) times. Manually loading the game and recording the state takes about 1-2 minutes. Since I don't have 1-2 million minutes of free time, I had to look for another approach.

So I decided to go for another approach: build a simulator which could accurately simulate a game's map, then use machine learning to run millions of simulations on that specific game map to find the map's most optimal score.

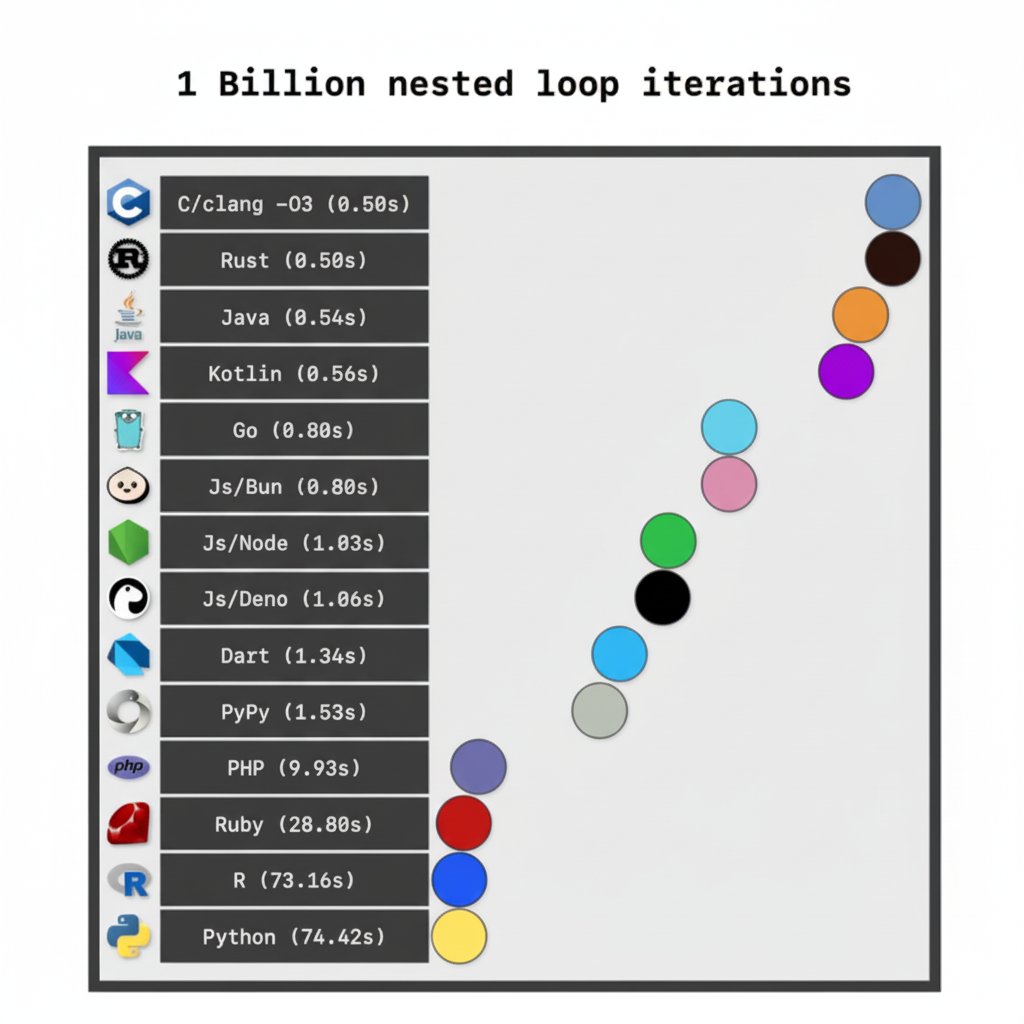
Speed Matters

So I started building the simulator in Python because I figured it would be simple and easy to build. Big mistake. Part way through building it, one of my friends brought up that speed would be of the utmost importance in this project. A difference in speed of the simulator of even a few milliseconds would be compounded over the millions of iterations I would need to run. Here's a cool graph online I found showing this problem:

Now I don't know C well enough to build this out, but I did several undergrad classes in Java, so I felt comfortable using that to build out the simulator.

The core of the simulator is built around an object-oriented design with two main components: the GameSimulator class and a hierarchy of Tile objects. Each tile type (buildings, power plants, mud, spike traps, etc.) inherits from an abstract Tile class and implements its own behavior when a cat steps on it. For example, when a cat stomps a building, the building awards power based on its size (250 for small houses, 500 for big houses), destroys its top floor, and executes any command attached to that floor.

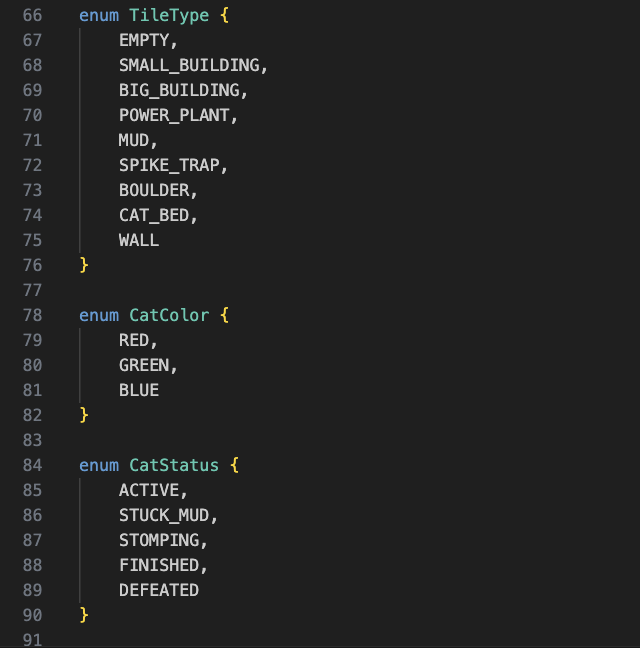
The game runs for 15 turns. The movement system operates in three distinct phases.

• ACTIVE state calculates where it wants to move based on its current direction. If a cat is facing EAST, it plans to move one tile to the right.
• STUCK_MUD cats skip their movement but clear their stuck status for next turn
• STOMPING cats stay in place to destroy the next floor of their current building.

The second phase is collision detection and movement resolution. When a cat tries to move, the simulator first checks if the target tile is passable. Walls (represented by #) and boulders (X) are impassable, so if a cat tries to move into one, it immediately reverses direction. If multiple cats try to move to the same tile in the same turn, there's a fight. The winner is determined first by current power. If there's a tie in power, hierarchy breaks it: Blue beats Red beats Green.

The third phase is where tile effects apply. Landing on a building causes the cat to stomp it and power is gained based on the building. The cat destroys the top floor, and executes any command attached to that floor. The simulation can end early if all cats either reach:

• FINISHED status (made it to their bed)
• DEFEATED status (lost all their power)

Otherwise it runs for exactly 15 turns.

And here is how I structured the input and output:

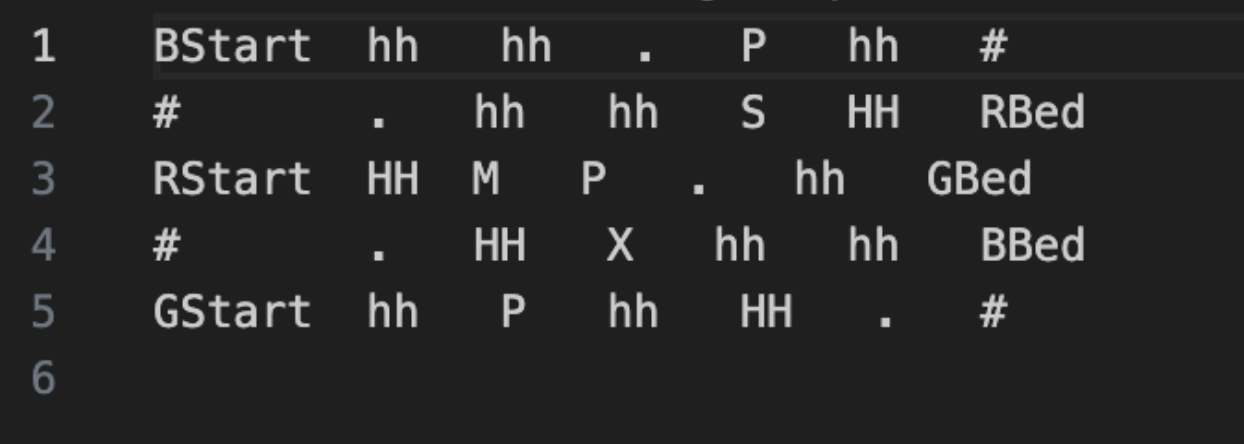
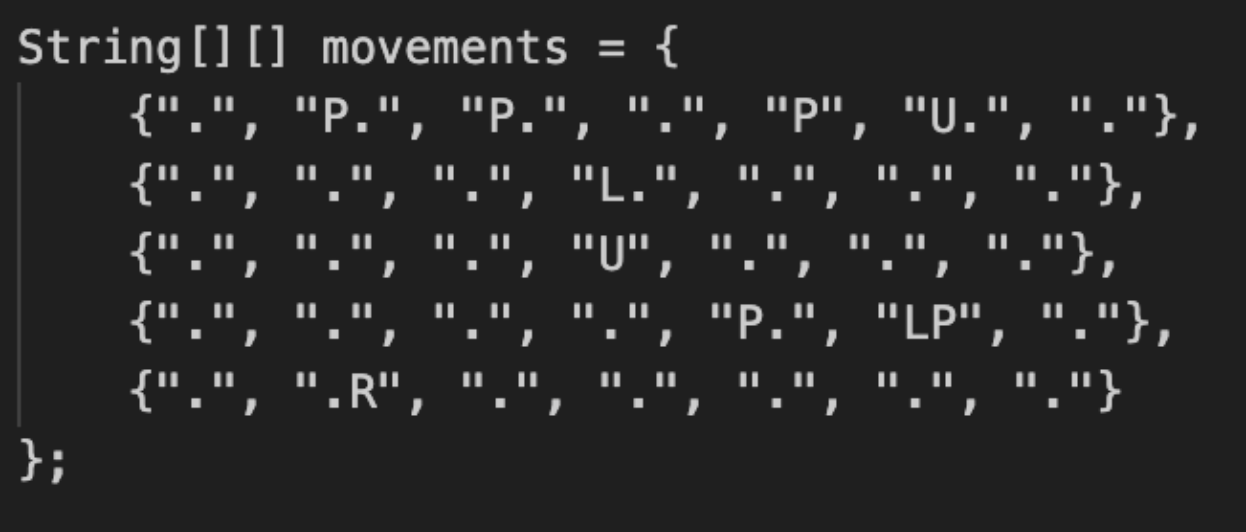
After running the simulator and comparing the output and intermediate steps with the real Kaiju game, tweaking the simulator a bit as I found small bugs, I ultimately ended up getting something that worked perfectly.

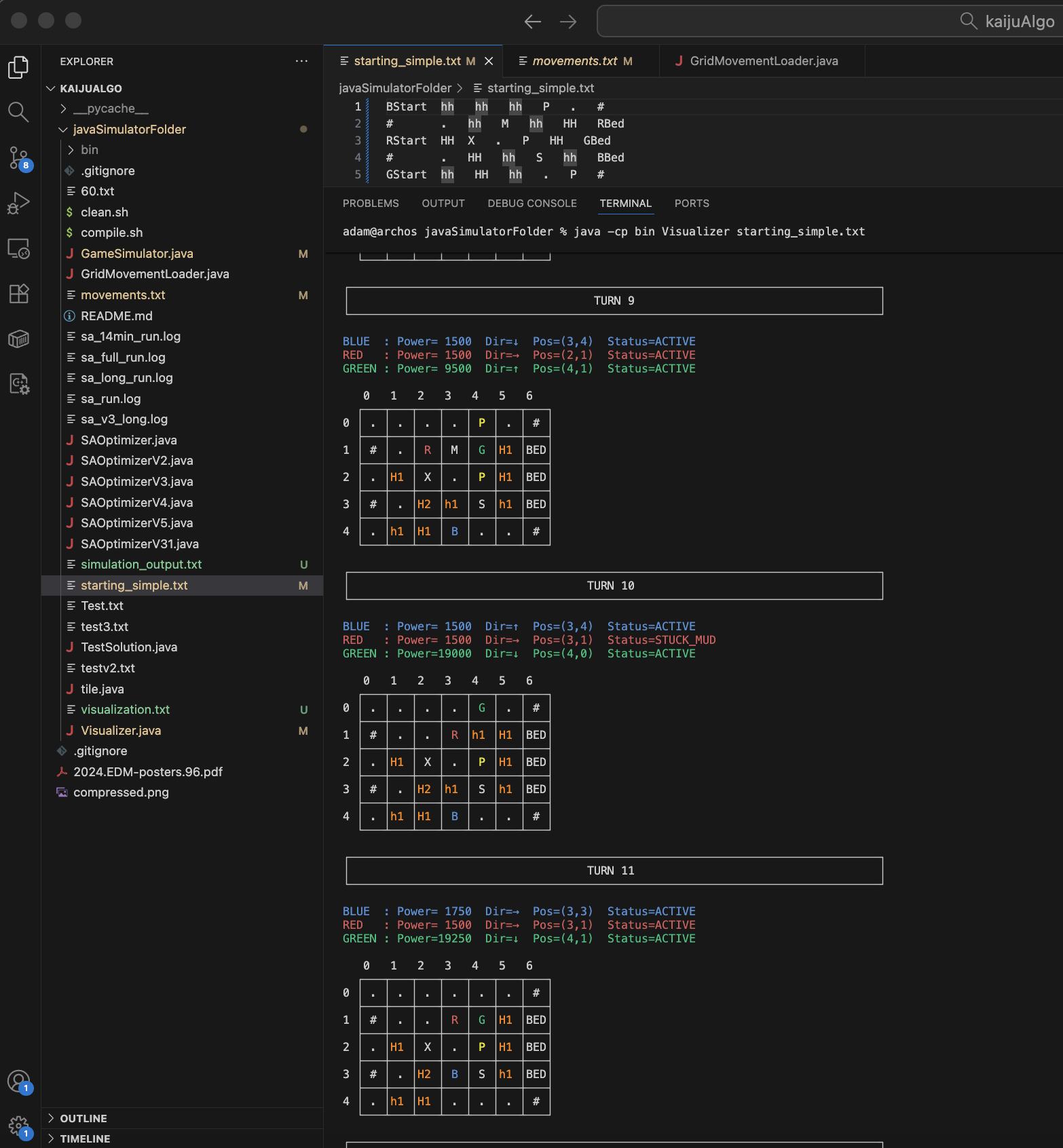
The Machine Learning

This was ultimately the make or break of this project. The number of possibilities was enormous. I had to rule out a few algorithms from the start. Because there was no adversary in this exercise, we could not use alpha-beta pruning like chess algorithms commonly use. Also since there is really no way to label data (and no efficient way to do so), approaches like Random Forest or K-nearest neighbors would not work.

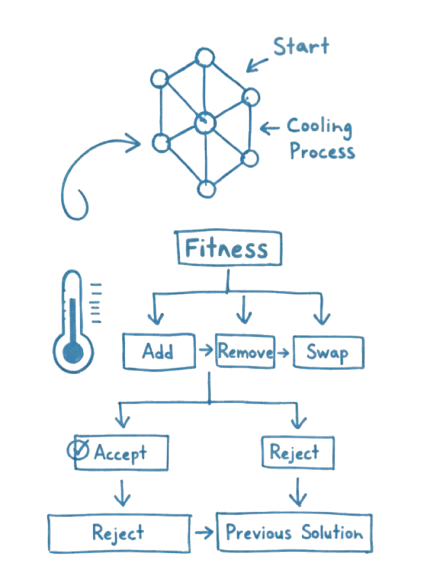
Bouncing around ideas with my friend Kevin, we ultimately decided simulated annealing would work best. The idea behind simulated annealing is like the real metallurgical process: heat everything up and let it cool down. By heating everything up, we mean trying a lot of random possibilities across a lot of different sequence types. Then by cooling down, we mean narrowing in on what worked best and optimizing that.

Simulated annealing works well here because of the nature of the game. The game has a lot of "good but not great" solutions. Solutions that get you 30-40k points, but are far from the optimal solution. However, usually once you find some 30-40k solution, you can usually optimize it better to get a better score of around 70-80k. The advantage of simulated annealing was that you can try a lot of different paths, find some "good but not great solutions" and then the cool down would be able to optimize it.

So that's exactly what I did. I created a basic simulating annealing algorithm.

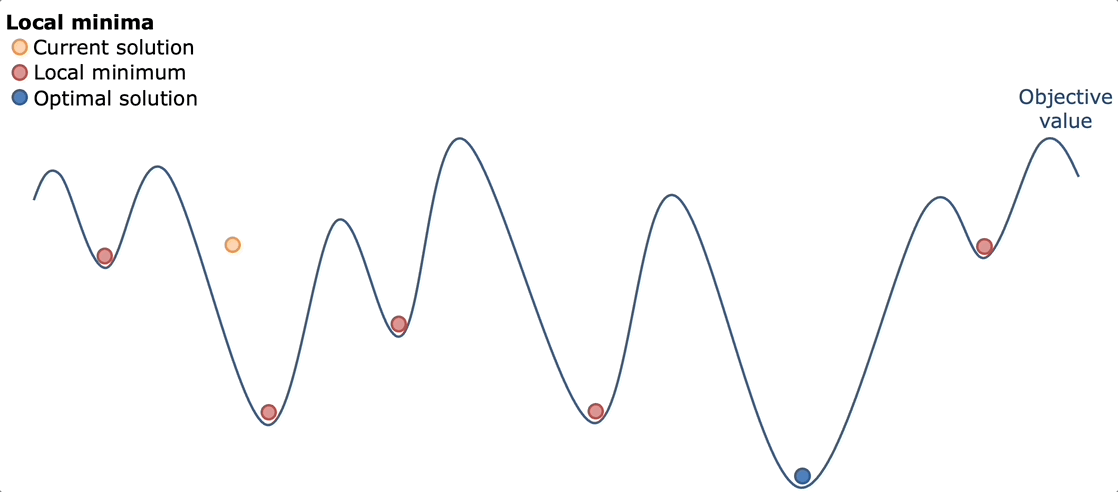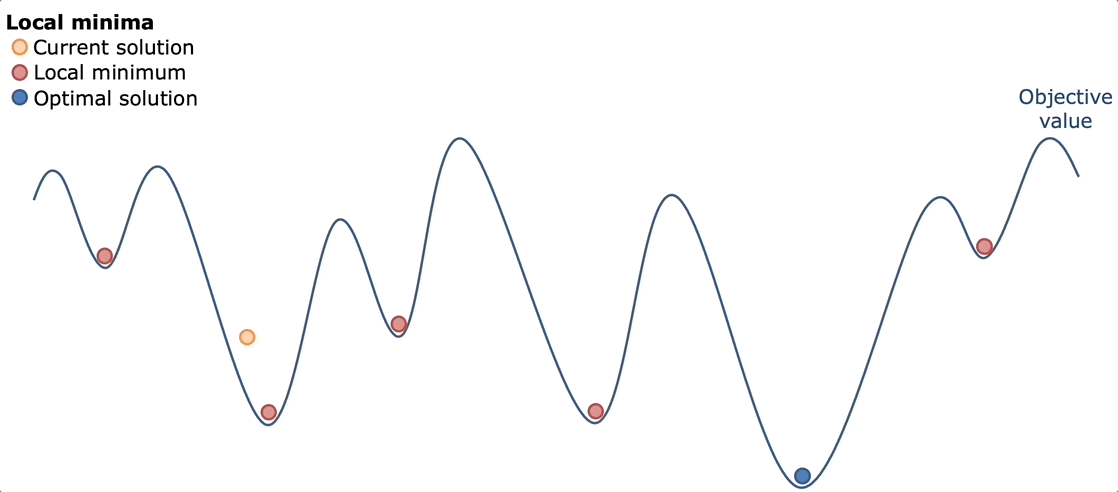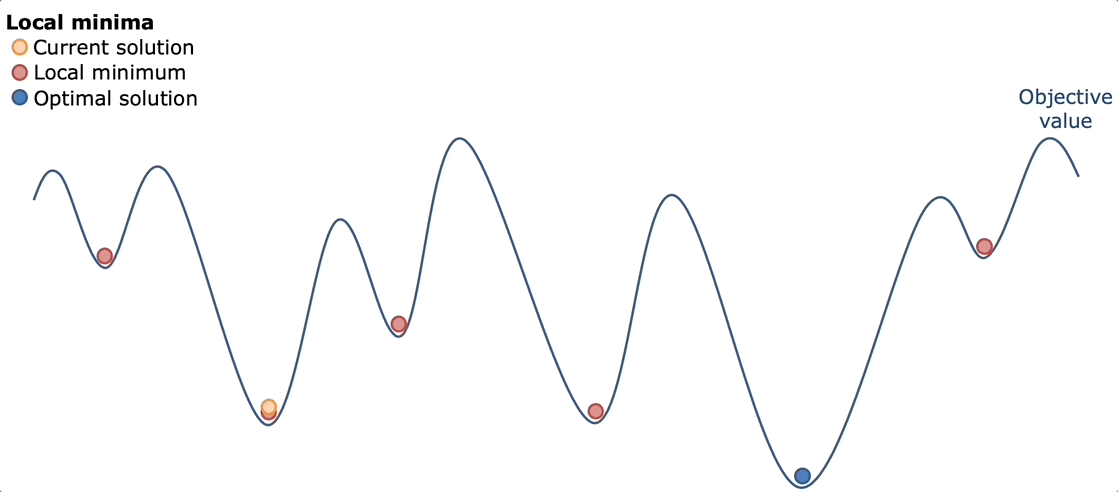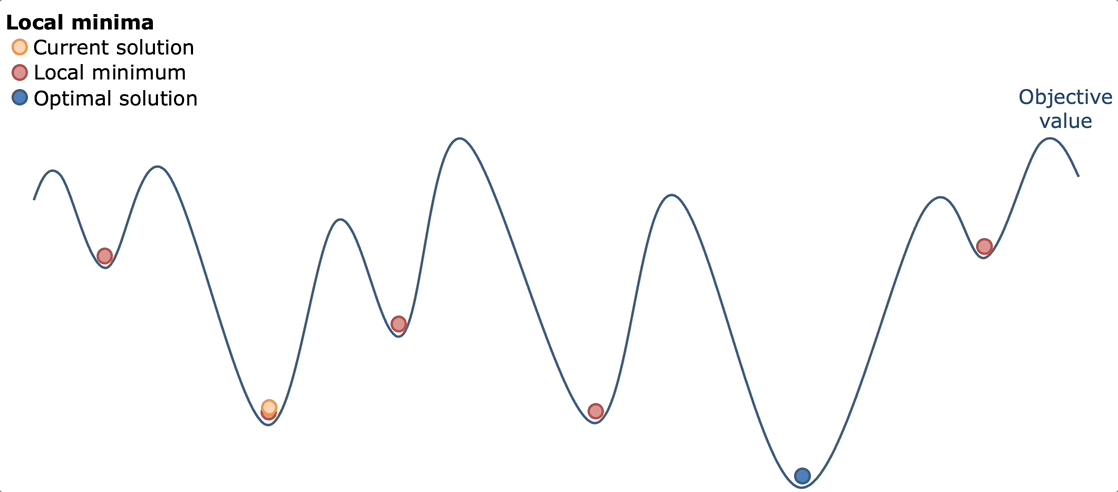
Pure Simulated Annealing

My first implementation followed the textbook simulated annealing approach with absolutely no heuristics or domain knowledge. The algorithm started with an empty solution (no commands placed) and iteratively improved it through random mutations. At each step, it would randomly choose to either
(1) remove a command
(2) add a new random command to any valid tile
(3) modify an existing command
(4) make 2-3 changes at once.

The acceptance criterion was pure simulated annealing: always accept better solutions, and accept worse solutions with probability e^{(ΔE/temperature)} where ΔE is the change in score. The temperature started extremely high (100,000) and cooled very slowly over millions of iterations, with an automatic restart mechanism that would reset from scratch every 10,000 iterations without improvement.

But…..the results were consistently disappointing. The algorithm would quickly climb from 0 to around 30,000-40,000 points in the first thousand iterations, then slowly creep up to 45,000-50,000 over the next few thousand iterations, before completely flatlining. Different runs would converge to different mediocre solutions, usually in the 40k-50k range, with occasional lucky runs hitting 60k-70k.

Given that high scores for this game can get up to 100k+, this was just not good enough.

After some time struggling with why this wasn't working, I realized this failure came down to a mismatch between how simulated annealing explores and what this problem actually required. First, the search space was absolutely massive. Most random command placements produced terrible scores because random turns would send cats into walls or spike traps, random powerups would be placed where cats never walked, and random stomps would destroy buildings cats needed for navigation. The algorithm spent the vast majority of its time wandering through the wasteland of 5k-30k score solutions, occasionally stumbling onto the 40k-50k "mediocre plateau" where one cat successfully reached its bed.

But the real killer was that single-command mutations were far too small to escape these plateaus. Getting from 40k to 100k+ required coordinated changes, not just pure random simulation. If you wanted three cats in bed to trigger the 3x and 5x multipliers, it meant building paths that required 3-5 turn commands working together and cats making it far into the playing field.

Without any heuristic, the search wandered aimlessly through the plateau. The cooling schedule made things worse: escaping a 40k local maximum to reach the 120k+ global maximum often required temporarily dropping to 20k-30k while rearranging commands, but once the temperature dropped low enough, the algorithm refused to make these necessary sacrifices.

The Optimization

After the disappointing results from the naive approach, I took a step back.

How did I find good solutions when I played the game?
Getting all the cats in the bed. This is a sure way to get a "pretty good" score, since that last cat gets a 5x multiplier. All pretty good to amazing scores had all cats in the bed.

So instead of using just score, I created new way to compare outcomes of simulated annealing:

The idea was to penalize the routes that did not lead cats closer to their beds. Now a 40k solution with cats close to beds (distance=5, fitness=37,500) was seen as significantly better than a 40k solution with cats far away (distance=20, fitness=30,000), even though they had identical game scores.

In essence, this new heuristic would "pull" the simulated annealing towards the solutions where the cats became closer and closer to the beds.

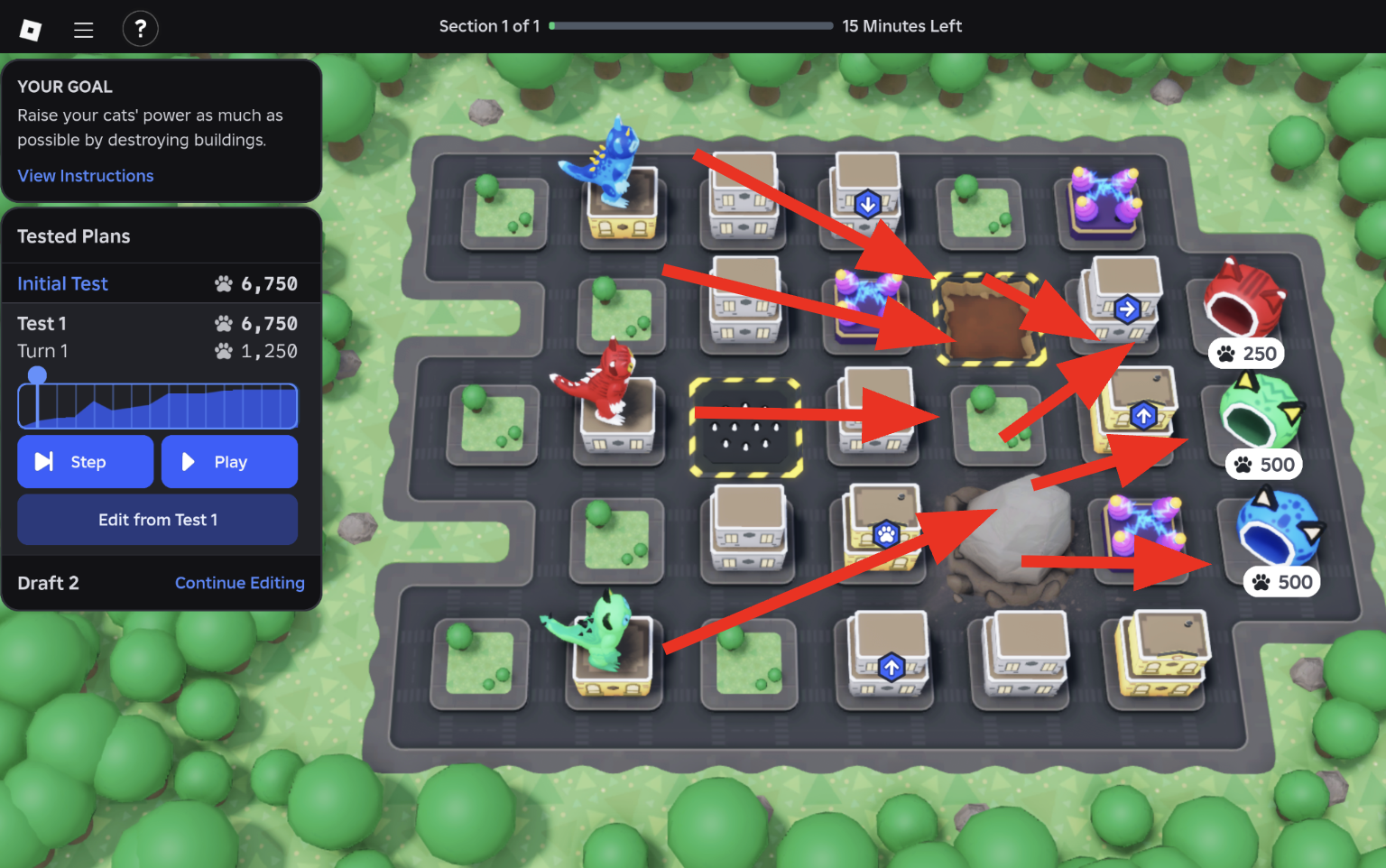
The algorithm gained a gradient to follow. It could "see" progress toward the goal even when the score was stuck. Crucially, this gave the algorithm patience during rearrangements: when modifying commands to build a better path, the score might temporarily drop, but if cats were getting closer to beds overall, the fitness would improve and the change would be accepted.

Then a small change was to adjust cooling for a number of iterations. So a 1 minute run would cool faster than a 5 minute run.

The results were dramatic. Where the naive approach consistently stalled at 40k-50k, the new approach had its first run of a score of 121,000!!

The distance heuristic guided the search toward regions where all three cats could reach their beds, unlocking the massive score multipliers (3× for second arrival, 5× for third arrival) that made 100k+ scores possible.

The idea for this optimization actually is the same heuristic which guides algorithms like Google Maps to find the best solution. That's a separate topic but I have a whole site exploring how that works.

The Final Optimization

While my algorithm could find great scores of 120k or even 140k, it still wasn't the best. How did I know this? Me and my friends could usually find a better solution if we worked together.

I started looking through the output of the simulated annealing. I realized for a 10 minute run, a best score was usually found in the first minute or two. Then it never changed. What was happening is that the algorithm was getting "stuck" in local maxima and never exploring the better maximas.

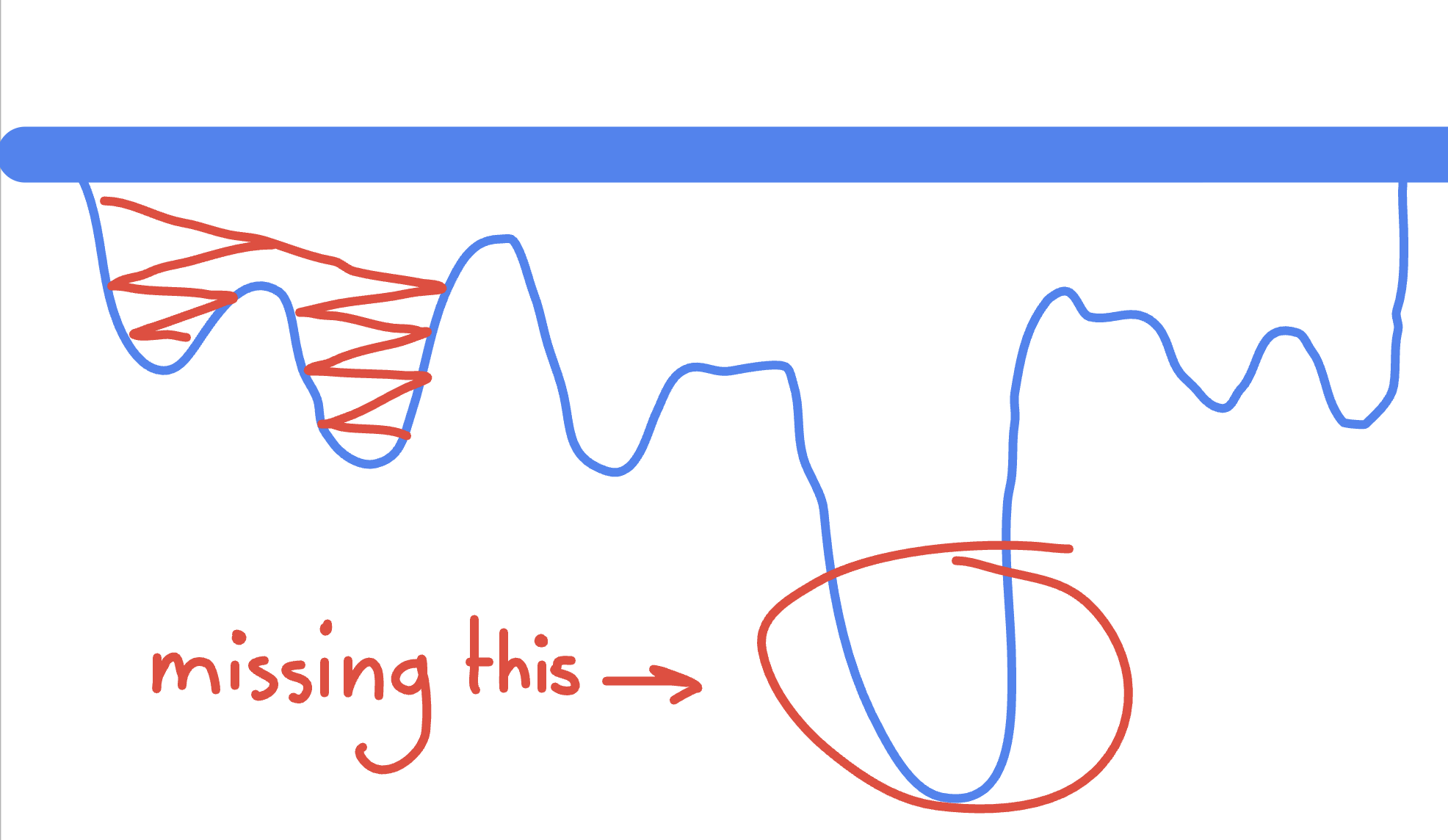
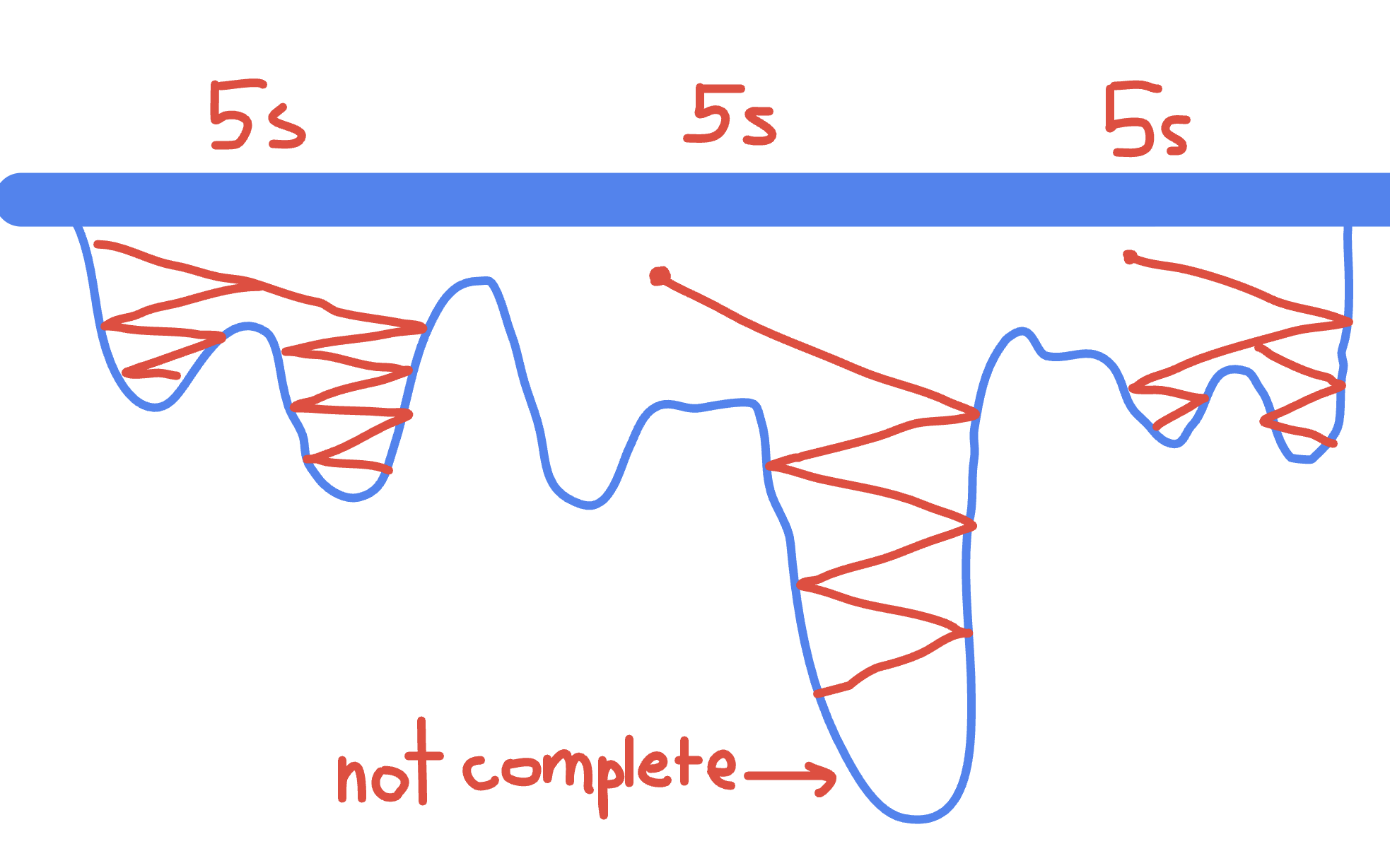
So instead of doing a full 10 minute run and letting it cool down too much to where it was exploring too many unviable paths, I did runs of smaller time frames to get more "random starts". This would allow me to explore a bunch of different paths instead of just one path, but very widely. I messed around with different times on the same map and I found 5 seconds was too short (good paths weren't fully discovered). And then 10 seconds and 15 seconds gave roughly the same results.

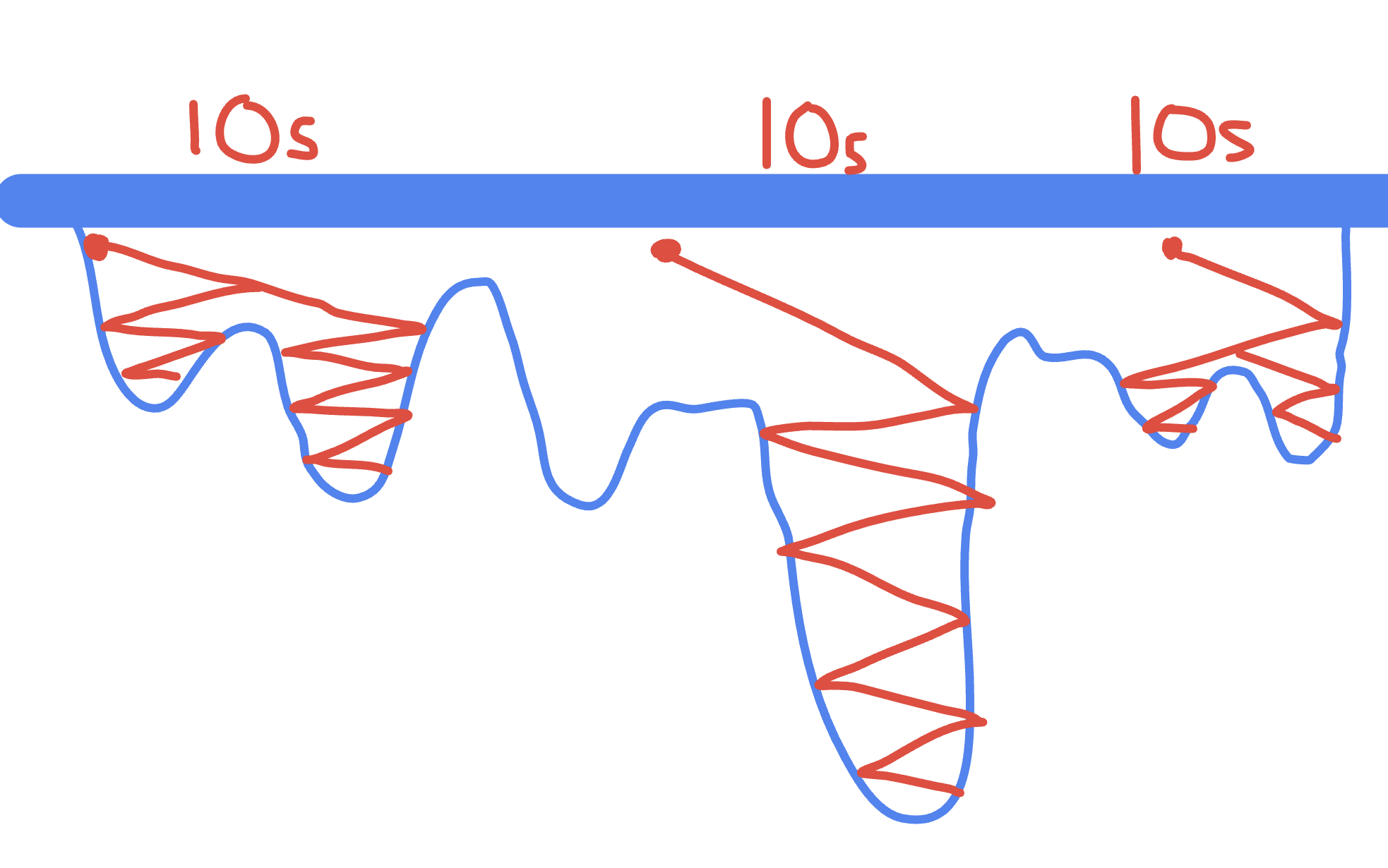
By restarting from a random point many times, the algorithm was able to get a better chance of finding those 150k+ divots. By also adding multithreading (running these random points in unison on multiple CPU threads), I greatly expanded my computational power. And with that, I was getting scores that were really good. I mean really really good.

Results

I did 10 test runs with the final version of simulated annealing, giving my algorithm about 10 minutes of compute, with 5 minutes reserved for me to be able to input the game map into my program and then copy the program's results back into the game.

Hardware: Macbook Air M2 (2022)
Compute Time: ~10 minutes
Paths Explored each Time: ~50,000,000 (a small fraction of 6³¹ possibilities)

Putting it to the Test

Here is a sequence of 10 consecutive runs of my algorithm to give you an idea of how it performs over a wide range of maps:

My algorithm achieved the following scores across 10 consecutive runs:

155,125 | 185,625 | 97,000 | 215,000 | 85,375
197,375 | 215,000 | 134,625 | 102,000 | 204,125

To put this in perspective, based on data published by Roblox, the average on-task submission score for candidates is 40,827 (± 21,056). My algorithm's mean score of 159,125 represents a 2.9x improvement over the human average, playing better than 99.999999% of people.

Key Takeaways

The lesson here echoes a fundamental truth across AI: raw computational power needs guidance. Deep Blue didn't defeat Garry Kasparov through brute force alone. It had chess grandmasters encoding years of strategic knowledge into its evaluation function, teaching it that controlling the center matters and king safety is crucial.

My simulated annealing optimizer followed the same arc. The naive version was directionless, wandering through mediocre 40k solutions. The distance heuristic, one simple insight that "cats near beds are valuable", transformed everything. It gave the algorithm vision, a way to recognize progress even when scores plateaued. Results improved 2-3x almost immediately, jumping from 40k-50k to 100k-120k+. Then with testing and observation of the simulated annealing, tweaking the core algorithm allowed for the performance to find the truly high results.

Since my algorithm doesn't explore all the possible paths, the game technically isn't "solved". There could hypothetically be better paths that my algorithm has not explored. Nevertheless, I've never seen a score greater than 215,000 ever. I think that might be the best score possible. And I don't even think its possible to get that high of a score on certain maps. So I think its safe to say the game is "beat" but not solved.

Ethics Disclaimer

I never used this algorithm to cheat on Roblox's assessment. I developed it much later after I took the assessment. However, I am 99%+ confident this algorithm could pass the Roblox interview Kaiju Cats game. As much as I love sharing my ideas with people, to prevent applicants from using this on the actual Roblox assessment, I have decided to keep this Github repo private.

While I didn't end up making it through the entire Roblox process, I ended up learning a lot about ML.

Could LLMs do better?

I decided to see if AI could do better. After I gave Claude the context of the game and the rules I prompted: "Be free, you no longer need to use simulated annealing. Find the best algorithm: it can be either improving my simulated annealing or a completely new approach. I expect a score of 100k+ within 5 minutes of computation."

Claude came up with an elaborate Genetic algorithm and I wrote some code to test it. The results: extremely disappointing. Claude's best approach: Genetic Mutation Algorithm.

Population: Start with 200 random solutions
Selection: Pick best solutions as "parents" (survival of fittest)
Crossover: Combine two parents to create "child" solution
Mutation: Randomly change some children
Repeat: Evolve for 2000 generations

Best scores: 20k-30k range

While LLMs are good for formatting and basic code, they struggle to understand games that require intuition.

Other Potential Ideas

Maximizing the number of powerplants one cat could get. In the very best scores, you "sacrifice" the 2 cats in the bed as fast as possible and then take the last cat and try to get the maximum score and the maximum number of powerplants with that cat. I briefly tried doing this, but with little improvements.